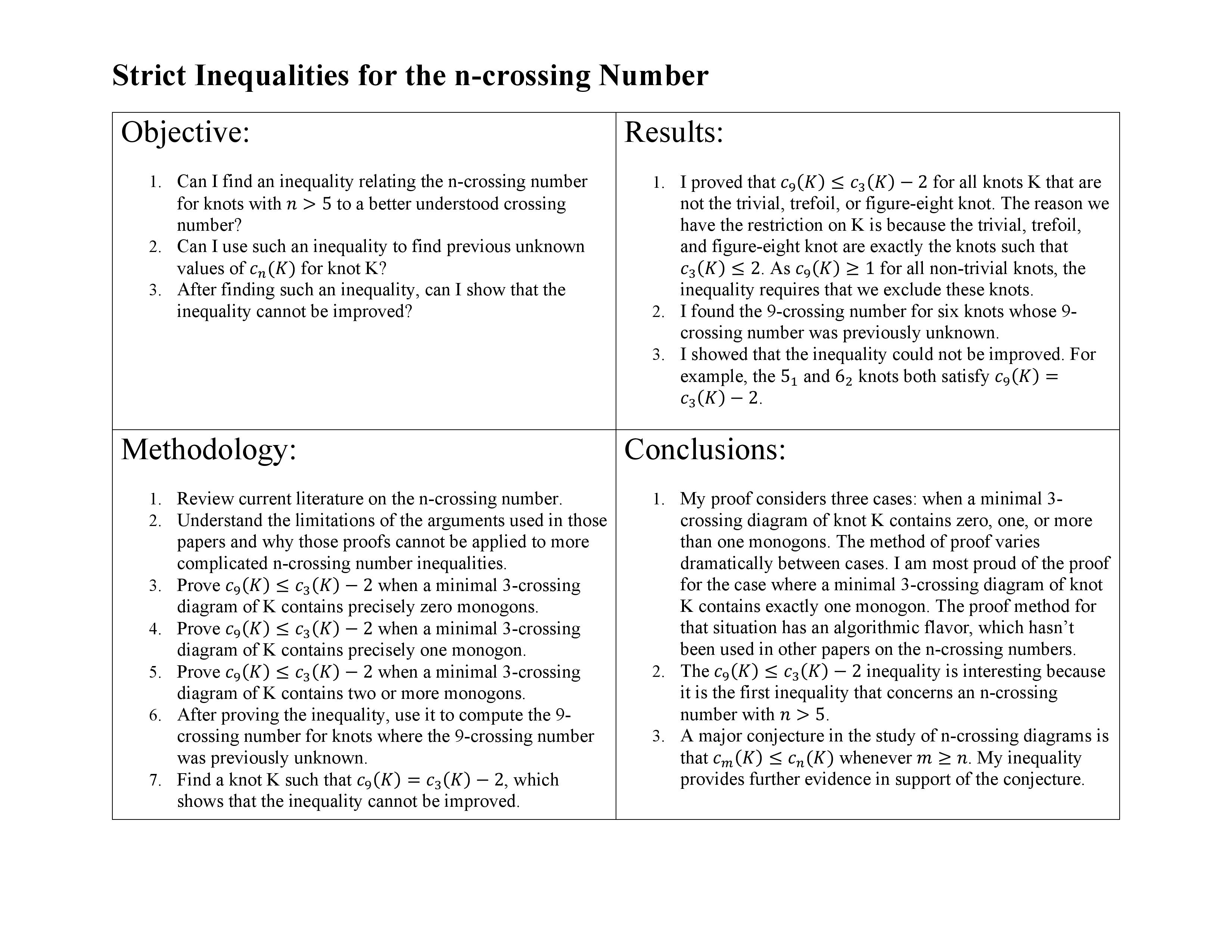
Strict Inequalities for the n-crossing Number
Abstract:
Bibliography/Citations:
C. Adams. Triple Crossing Number of Knots and Links, Journal of Knot Theory and
Its Ramifications. Vol. 22, No. 02, 1350006 (2013).
C. Adams. Quadruple Crossing Number of Knots and Links, Mathematical Proceed-
ings of the Cambridge Philosophical Society, Vol. 156, Issue 2, 1350006 (2014).
C. Adams, J. Hoste, M. Palmer. Triple-crossing number and moves on triple-crossing
link diagrams, Journal of Knot Theory and Its Ramifications. Vol. 28, No. 11, 1940001
(2019).
C. Adams, O. Capovilla-Searle, J. Freeman, D. Irvine, S. Petti, D. Vitek, A. We-
ber, S. Zhang. Multi-crossing number for knots and the Kauffman bracket polynomial,
Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 164, Issue 1
(2016).
C. Adams, O. Capovilla-Searle, J. Freeman, D. Irvine, S. Petti, D. Vitek, A. Weber, S.
Zhang. Bounds on ̈ubercrossing and petal numbers for knots, Journal of Knot Theory
and Its Ramifications. Vol. 24, No. 02, 1550012 (2015).
C. Adams, T. Crawford, B. DeMeo, M. Landry, A. Lin, M. Montee, S. Park, S.
Venkatesh, F. Yhee. Knot projections with a single multi-crossing, Journal of Knot
Theory and Its Ramifications. Vol. 24, No. 03, 1550011 (2015).
M. Jablonowski. Tabulation of knots up to five triple-crossings and moves between
oriented diagrams, preprint at ArXiv:2105.10921 (2021).
M. Jablonowski. Triple-crossing number, the genus of a knot or link and torus knots,
Topology and its Applications. Vol. 285, 107389 (2020).
M. Jablonowski, L. Trojanowski. Triple-crossing projections, moves on knots and links
and their minimal diagrams, Journal of Knot Theory and Its Ramifications. Vol. 29,
No. 04, 2050015 (2020).
Additional Project Information
Project files
Research Plan:
1. Fully review current literature on the n-crossing number.
2. Understand the limitations of the arguments used in those papers and why those proofs cannot be applied to more complicated n-crossing number inequalities.
3. Gain an intuition for the n-crossing number and conjecture a fifth inequality for the n-crossing number.
4. Break down the conjecture into individual cases.
5. Prove each of those individual cases, which in turn proves the inequality.
6. Use the inequality to compute previously unknown values of the n-crossing number.
7. Find a knot that realizes the upper bound of the inequality, which shows that the inequality cannot be improved.
Questions and Answers
1. What was the major objective of your project and what was your plan to achieve it?
a. Was that goal the result of any specific situation, experience, or problem you encountered?
b. Were you trying to solve a problem, answer a question, or test a hypothesis?
The driving goal behind knot theory is to find functions that can tell apart different mathematical knots. A promising new family of functions, called the n-crossing numbers, was introduced by Professor Colin Adams in 2013. Though these functions can distinguish between many different knots, we currently know very little about them: relations between these n-crossing numbers are largely unknown, and we lack the computational ability to determine the n-crossing number for large values n. In an effort to understand and compute these functions, mathematicians have proved inequalities relating the different n-crossing numbers. Inequalities have been found for the 2-, 3-, 4-, and 5-crossing numbers. After I read Professor Adams’ The Knot Book (1994), I became interested in both knot theory and Professor Adams’ current research, and began thinking about problems in the field. The goal of my research was to find an inequality for a more complicated crossing number, which would both aid in the computation of said crossing number and help mathematicians learn more about these complicated functions. I was primarily trying to answer the question, “what other inequalities exist between the n-crossing numbers?”
2. What were the major tasks you had to perform in order to complete your project?
a. For teams, describe what each member worked on.
My main goal was to prove my conjecture that c9(K) ≤ c3(K) – 2. To get there, I broke up this conjecture into three cases: the case where a minimal triple-crossing diagram of K contains zero monogons, the case where such a diagram contains one monogon, and the case where such a diagram contains two or more monogons. Each case required a different method of proof and coming up with these novel proofs took months.
3. What is new or novel about your project?
a. Is there some aspect of your project's objective, or how you achieved it that you haven't done before?
b. Is your project's objective, or the way you implemented it, different from anything you have seen?
c. If you believe your work to be unique in some way, what research have you done to confirm that it is?
Inequalities concerning n-crossing numbers for n > 5 were not previously known. I have been in contact with Professor Colin Adams, the leading expert in the study of n-crossing numbers. He has confirmed the novelty of my results.
4. What was the most challenging part of completing your project?
a. What problems did you encounter, and how did you overcome them?
b. What did you learn from overcoming these problems?
The most challenging part of completing the project was coming up with a proof of my theorem. My results were novel, meaning I had to think of original and complicated proofs. On multiple occasions, I would realize that an argument had one small mistake. But even the smallest mistakes undid the entire project. Each time, I managed to find some other way to proceed, even if it meant losing weeks of progress. These setbacks taught me the importance of persistence.
5. If you were going to do this project again, are there any things you would you do differently the next time?
I read many of the papers relevant to my research while actively working on my project. If I were to complete a similar research project again, I would begin by reading through all the relevant papers before beginning the research phase. This separation of reading and research phases would have saved time, as I spent multiple weeks thinking about a problem until eventually realizing someone had already solved it.
6. Did working on this project give you any ideas for other projects?
Yes! My proof that the 9-crossing number is strictly less than the 3-crossing number minus two relies heavily on the 5-crossing number as a middleman between the two other crossing numbers. I converted certain 3-crossing diagrams of knots into 5-crossing diagrams, and then into 9-crossing diagrams. I’m now interested in finding an inequality between the 5-crossing number and 9-crossing number; such a theorem would generalize my main result.
7. How did COVID-19 affect the completion of your project?
Because my project was primarily done with paper and pencil at home, COVID-19 did not affect my project’s completion.